hypothesis - property based testing¶
quick recap - unit testing¶
- unit
- written by programmers
- fast
pytest demo - 01_test_code_add.py¶
- ill defined tests
- repeated code
This is what frameworks are for
pytest demo - 02_test_code_add_param.py¶
All tests are passing!
Does it work?¶
def test_add_numbers_zero_and_one():
assert add_numbers(0, 121) == 121
def add_numbers(n1, n2):
if (n2 % 11) == 0 and n1 == 0:
return n1
return n1 + n2
What should we be testing?¶
The addition operator properties
Commutativity¶
$a + b \equiv b + a$
Associativity¶
$a + (b + c) \equiv (a + b) + c$
Identity¶
$a + 0 = a $
# %load 03_test_add_hypothesis.py
from hypothesis import given
from hypothesis import strategies as st
from code_add import add_numbers
@given(st.integers(), st.integers())
def test_code_add_commutativity(a, b):
assert add_numbers(a, b) == add_numbers(b, a)
@given(st.integers())
def test_code_add_identity(a):
assert add_numbers(a, 0) == a
@given(st.integers(), st.integers(), st.integers())
def test_code_add_associativity(a, b, c):
assert add_numbers(
a,
add_numbers(b, c)
) == add_numbers(
add_numbers(a, b),
c
)
hypothesis¶
QuickCheck¶
1 - Assertions are written about logical properties that a function should fulfill
2 - QuickCheck attempts to generate a test case that falsifies such assertions
3 - QuickCheck tries to reduce it to a minimal failing subset by removing or simplifying input data that are unneeded to make the test fail
End user POV
- A fuzzer
- A library of tools for making it easy to construct property-based tests using that fuzzer
Dissecting our example¶
from hypothesis import strategies as st
Most things should be easy to generate and everything should be possible.
help(st.integers)
Help on function integers in module hypothesis.strategies._internal.core:
integers(min_value=None, max_value=None)
Returns a strategy which generates integers; in Python 2 these may be
ints or longs.
If min_value is not None then all values will be >= min_value. If
max_value is not None then all values will be <= max_value
Examples from this strategy will shrink towards zero, and negative values
will also shrink towards positive (i.e. -n may be replaced by +n).
from hypothesis import given
help(given)
Help on function given in module hypothesis.core:
given(*_given_arguments, **_given_kwargs)
A decorator for turning a test function that accepts arguments into a
randomized test.
This is the main entry point to Hypothesis.
the good stuff¶
- pytest integration
- strategies for most common types
- composite strategy to generate new strategies
- compositional shrinking of examples
- a database of failing examples to check regressions
- read this Anatomy of a Hypothesis Based Test
- Hypothesis for the Scientific Stack: pandas/numpy strategies
Some cool examples*¶
* The opinions expressed on this slide are my own and not necessarily those of my employers
Sorting¶
sort(l) returns a listsorted list has the same elementsthere is an ordering between elementssorting a sorted list does not change anything
The more things change, the more they stay the same
There and back again¶

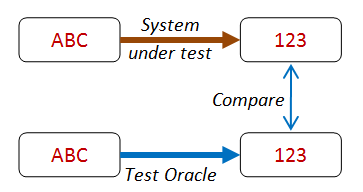
Test oracle¶
The change making problem¶
Let $S = \{w_1, w_2, \ldots, w_n \mid w_i < w_j \forall i < j, w_i \in \mathbb{Z}^+ \}$ a coin system ($1$ should always be present)
Let $W \in \mathbb{Z}^+$.
Let $x_i$ be the amount of coins of denomination $w_i$
$ \begin{equation*} \begin{aligned} & \text{minimize} & & \sum_{j=0}^{n}(x_j) \\ & \text{subject to} & & \sum_{j=0}^{n} w_j x_j = W \end{aligned} \end{equation*} $
And let $S$ be tagged as canonical if $G_r(W,S) = D_p(W,S) \forall W$ where $G_r$ is the solution provided by the greedy algorithm and $D_p$ the dynamic programming solution.
How can we find a non-canonical system?
A note on verbosity¶
What examples is hypothesis running?
We can see an example with a prime numbers generator